Last month I mentioned that I had more graphs to show you, so let me jump right in. In a previous column [May ‘08], I mentioned that audio taper pots aren’t really logarithmic in a true sense, but that they employ a trick that allows them to mimic a log taper. Of course, I just breezed right on past that statement with no helpful explanation, so allow me to expound.
There are audiophile-grade pots that I understand provide a very close approximation of a logarithmic curve, but they’re large and expensive (and sometimes ganged – two pots in one – for stereo rather than mono applications), and aren’t suited to the guitar. Instead, guitar manufacturers almost universally use inexpensive pots that come from a handful of companies, such as CTS.
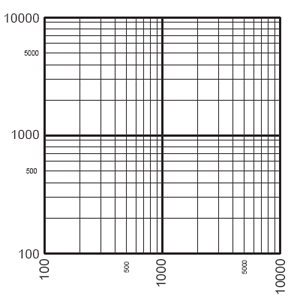
So as to clarify the difference between logarithmic data and non-logarithmic data, let me show you a Bode plot again (a logarithmic graph – this is the same graph shown last month), along with a second graph that shows some data in a non-logarithmic format.
 | |
|
100 = 1 x 102
1000 = 1 x 103
10,000 = 1 x 104
500 = 5 x 102
5000 = 5 x 103
Each major division line represents a tenfold increase in value. The relationship of 500 to 5000, or of 100 to 1000, or of 1374 to 13,740, is the same: it’s a tenfold increase. So the distances between these sets of numbers are the same; this graph is all about relationships.
Now look at this graph:
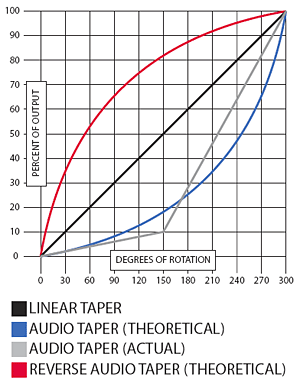 This graph is not logarithmic, it’s linear. That is, it shows a direct, linear correlation between the vertical scale and the horizontal scale. Obviously, you’ve seen tons of graphs that use this format.
This graph is not logarithmic, it’s linear. That is, it shows a direct, linear correlation between the vertical scale and the horizontal scale. Obviously, you’ve seen tons of graphs that use this format. This graph is not logarithmic, it’s linear. That is, it shows a direct, linear correlation between the vertical scale and the horizontal scale. Obviously, you’ve seen tons of graphs that use this format.
By the way, in case you hadn’t noticed, this second graph illustrates the trick employed by cheap guitar pots to mimic a true log curve. The graph’s vertical scale represents the output of a pot, from 0 to 100 percent. The pot’s value is irrelevant – this scale shows percentage values, not absolute values. The horizontal scale represents the 300 degrees of rotation for a typical CTS pot as used in the guitar industry.
The black line shows the plot that a linear taper pot would make. It’s perfectly straight: if you turn the pot 10 percent (30°) then you get 10 percent output. Turn it 70 percent (210°) and you get 70 percent output.
Now look at the blue line. This is what a true logarithmic plot would look like. You can see that you have to turn the pot pretty far before the output starts to rise appreciably. If you had a pot whose output truly followed this plot, then it would produce a perfect volume increase or decrease. That complaint you may have heard about some pots that act more like a switch than a pot, reducing volume suddenly and dramatically in a way that makes it difficult to control, wouldn’t apply to this pot at all. It would work perfectly.
But don’t hold your breath. The gray line is what you actually get in a guitar pot. The trick? Determine the pot’s midpoint value (typically 10 percent – remember last month’s column?) and then print two separate carbon sections – one on each side of center – to make up the overall trace. Oh, and make the two batches of carbon material that are used for the two sections have different resistive values. Clever, huh? You can see that the result, which is really two linear sections, does a moderately effective job of following the logarithmic plot that it’s designed to mimic. Of course, it’s far from perfect, but at $5 it’s the best you’re going to get, and it’s arguably good enough. I say arguably because it works and most people don’t notice that it’s not perfect. If you do, if you want better and aren’t afraid to pay for it, then it may be time to start rummaging through that audiophile parts bin down at the Wal-Mart.
Happy hunting!
George Ellison
Founder, Acme Guitar Works
acmeguitarworks.com
george@acmeguitarworks.com
772-770-1919













![Rig Rundown: Russian Circles’ Mike Sullivan [2025]](https://www.premierguitar.com/media-library/youtube.jpg?id=62303631&width=1245&height=700&quality=70&coordinates=0%2C0%2C0%2C0)













