Dear Sensei:
Can you please explain in detail how the seven modes work? I’m studying music theory on my own, and when I go online to research modes I’m often confused by what sometimes seems to be contradictory information.
Thanks,
Karl Mirabella
Dear Karl,
This is a topic many guitarists struggle with, so let’s see if we can shed some light on it. There are two ways to understand modes and each approach ultimately gets you to the same place. However, the two systems require a different mindset, and this can sometimes create confusion when you’re trying to reconcile info you may encounter on the web, or glean from another guitarist or music teacher.
When it comes to modes, we need to be very specific: In this lesson, we’ll drill down on the seven modes of the major scale. Other types of scales have modes too, but the major scale modes are by far the most common, so that’s what we’ll tackle here.
The “Relative” Approach
Our first way to look at modes involves playing through a single major scale from seven different starting points. But before we go any further, let’s review the basics.
Using a specific pattern of whole-steps and half-steps, you can build a major scale from any of the 12 tones of the Western music system. Here’s the pattern, which starts on a given root and ultimately ends an octave above it: Whole-step, whole-step, half-step, whole-step, whole-step, whole-step, half-step. This yields a series of eight notes. It can be easier to visualize this pattern when it’s written like this: W–W–H–W–W–W–H. That’s the shorthand we’ll employ in this lesson.
Here’s why looking at the arrangement of whole- and half-steps in the major scale is crucial to understanding modes: A major scale sounds the way it does because of where the whole- and half-steps occur within an octave. If you were to change the sequence of whole- and half-steps, the sound changes and you no longer have a major scale.
The seven major-scale modes have Greek names. We’ll address each one, starting with the first—Ionian. Sonically the Ionian mode is identical to the major scale—we’re simply using its Greek name. Fig. 1 shows a one-octave G Ionian pattern, with its low G root located on the 6th string, 3rd fret. Take a moment to play it ascending and descending: G–A–B–C–D–E–F#–G. Pay attention to the low and high roots, which are indicated in red. (If you’ve ever studied moveable solfège, this will sound familiar—our good old “do re me fa sol la ti do.”)
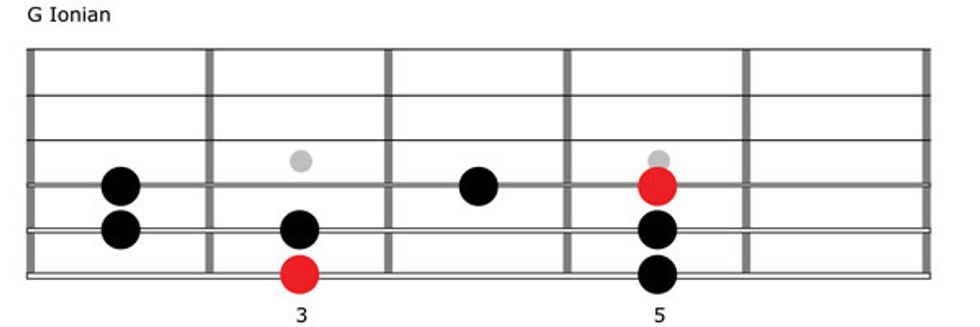
Now analyze what you’re playing in terms of whole- and half-steps. That’s right! Ascending from G, you’re laying down a W–W–H–W–W–W–H pattern.
All right, we’re now ready to step off the precipice.
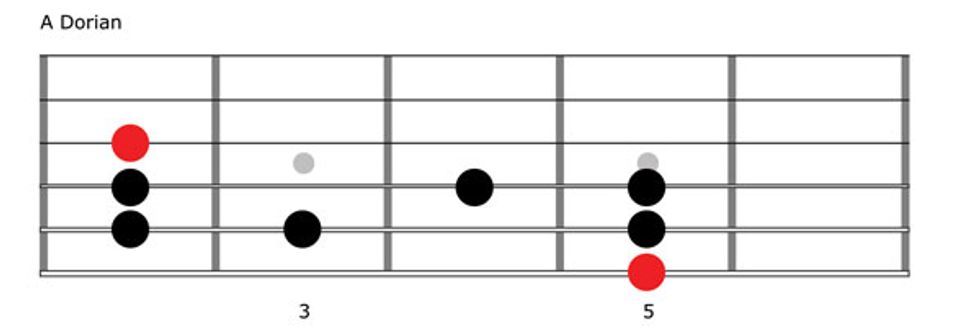
Now we’ll take the same string of notes we played as a G major scale, but instead of starting and ending on G, we’ll shift to the second tone—A—and use it to create a new one-octave pattern: A–B–C–D–E–F#–G–A. We haven’t changed any notes; we’re simply declaring A as the root. But by doing so, we’ve changed the pattern of whole- and half-steps to W–H–W–W–W–H–W. This arrangement is called the Dorian mode.
Fig. 2 shows a one-octave A Dorian pattern. As you play it ascending and descending a few times, really dig into the new A root. This will focus your ears on the Dorian sound, which is minor. Dorian is used extensively in jazz and rock for playing melodically over minor chords and vamps.
Note: At the end of this section, you’ll find a set of backing tracks that correspond to each of the relative modes we’re currently examining. These tracks will allow you to explore A Dorian, as well as the other modes of the G major scale, in a musical context.
Now we can see why we use the term “relative” to describe this system of understanding modes: We’re relating Dorian to the major (Ionian) scale we began with. In this case, we’re comparing A Dorian to G major, but you can apply this “start on the second tone to get Dorian” way of thinking to any major scale.
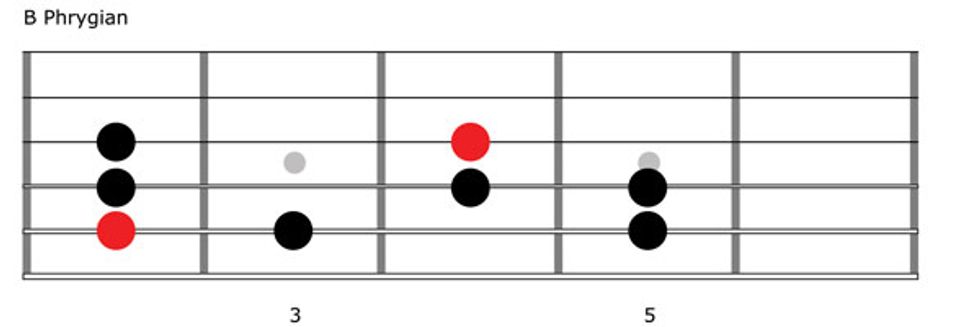
We’ll now shift to B, the third tone of G major, and use it as the root for our one-octave scale: B–C–D–E–F#–G–A–B. Again, the pattern of whole- and half-steps has shifted, and we now have H–W–W–W–H–W–W. This mode is called Phrygian. It also has a minor sound, but the half-step between the first two notes gives it a distinctly flamenco flavor (Fig. 3).
By now you’re probably getting the hang of this process and can anticipate our next move: Use the fourth tone (C) of our parent major scale as the launching pad. This yields C–D–E–F#–G–A–B–C. Its underlying pattern is W–W–W–H–W–W–H, and this arrangement of whole- and half-steps generates the Lydian mode. As you play through Fig. 4, notice how Lydian has a major sound, but with a spiky bump right in the middle of the sequence.
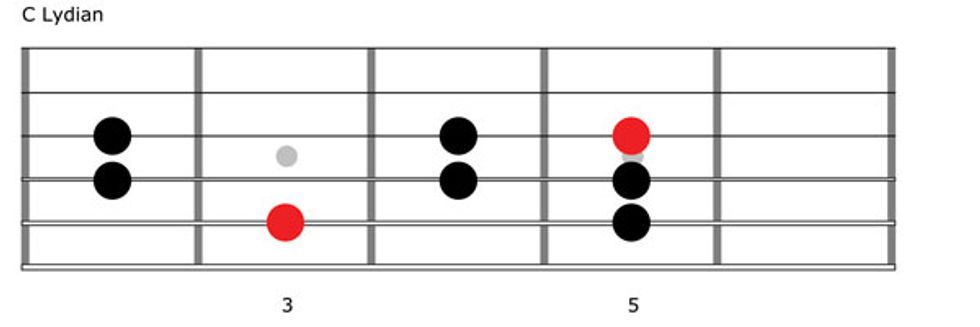
Moving on, we use the fifth tone of our parent major scale as the next root. In G major, this note is D, and it gives us D–E–F#–G–A–B–C–D. The pattern of steps between the notes is W–W–H–W–W–H–W, and this gives us the Mixolydian mode. Play through Fig. 5 to make friends with this sound, which is perfect for jamming over dominant vamps. Match the roots and you’re good to go (i.e., play D Mixolydian over a D9 vamp).
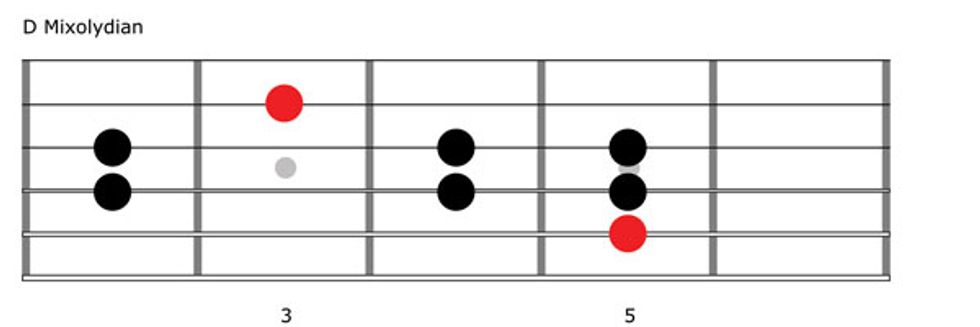
Again, let’s shift our root, this time to the sixth tone of our parent major scale. In G major, that’s E, so we have E–F#–G–A–B–C–D–E. This W–H–W–W–H–W–W pattern creates the Aeolian mode. Now work through Fig. 6. If it sounds familiar that’s because Aeolian is identical to natural minor, and you’ve probably played it many times.
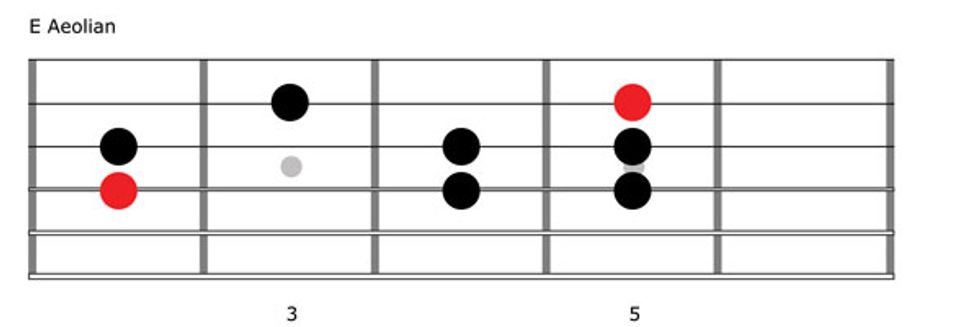
We’re almost done—just one more shift. It’s time to use the seventh tone as our root. Working from G major, this gives us F#–G–A–B–C–D–E–F#, and these notes correspond to a H–W–W–H–W–W–W pattern. This is called the Locrian mode, and in this case, we’re playing F# Locrian (Fig. 7).
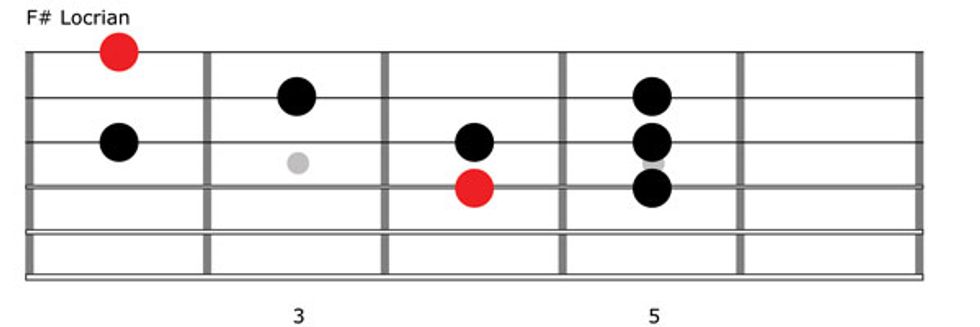
Okay, now that we’ve used each note of the G major scale as a root, we’ve worked through all seven of G major’s modes: G Ionian, A Dorian, B Phrygian, C Lydian, D Mixolydian, E Aeolian, and F# Locrian. Let’s summarize what we’ve just covered with a handy-dandy chart.
The Seven Modes of the G Major Scale
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G Ionian | G | A | B | C | D | E | F# | G | ||||||
| A Dorian | A | B | C | D | E | F# | G | A | ||||||
| B Phrygian | B | C | D | E | F# | G | A | B | ||||||
| C Lydian | C | D | E | F# | G | A | B | C | ||||||
| D Mixolydian | D | E | F# | G | A | B | C | D | ||||||
| E Aeolian | E | F# | G | A | B | C | D | E | ||||||
| F# Locrian | F# | G | A | B | C | D | E | F# |
It’s important to understand that every major scale contains its own relative Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian modes. This is why they’re called “modes of the major scale.” We used G major to illustrate the root-shifting process simply because it’s conveniently located on the fretboard. But this system holds true for any major scale, in any position or string set, anywhere on the fretboard. Be patient—it takes time to investigate the fretboard by unpacking every major scale pattern you know into its relative modes.
Here are the backing tracks we promised earlier. Pick one of the G major modes, review its fretboard pattern, as shown in Figures 1-7, match it to its corresponding backing track, and get busy improvising melodically. Once you master these one-octave patterns shown here, work them out in other areas of the fretboard, and again improvise using the corresponding backing track to accompany you.
The “Parallel” Approach
We’re now going to examine a completely different strategy for generating modes. Once again we start with the major scale, but this time we’ll apply a set of formulas to it, thus changing its internal whole- and half-step construction. To create our seven different modal formulas, we first need to express the one-octave major scale numerically: 1–2–3–4–5–6–7–8.
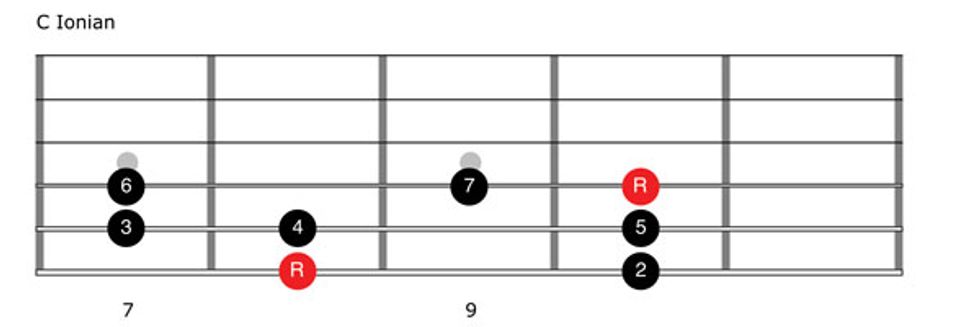
This is the formula for our first mode, Ionian. Fig. 8 shows a one-octave C Ionian pattern (C–D–E–F–G–A–B–C) with its root on the 6th string, 8th fret. (Remember, the terms “root” and “1” are interchangeable. To keep the fretboard charts consistent, we’re again showing the root in red.) In Clip 1, you’ll hear C Ionian played over a low C drone. We’ll use this drone as a sonic foundation for our subsequent modes, which again will be Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian. But this time each mode will have the same root—C. By using the identical starting point you’ll be able to both hear and visualize the differences between each mode.
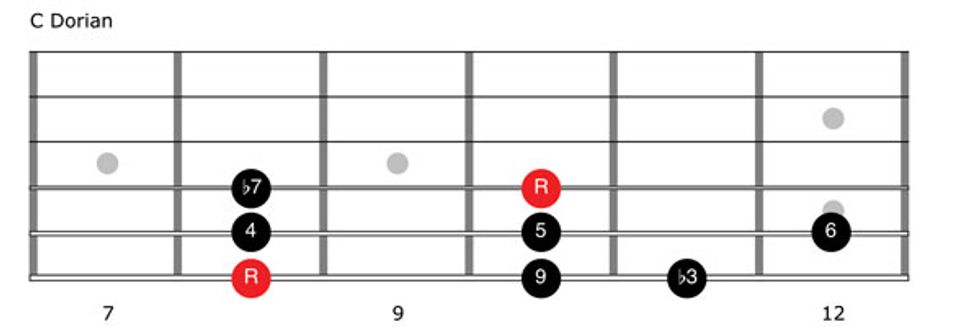
Compared to a one-octave major scale starting from the same root, the formula for the Dorian mode is 1–2–b3–4–5–6–b7–8. By applying this formula to C major (Ionian), we get C Dorian, or C–D–Eb–F–G–A–Bb–C.
Fig. 9 shows C Dorian in the 8th position. You can see that we’ve lowered two tones by a half-step, which means the difference between Ionian and Dorian is 3 and 7, versus b3 and b7, respectively. The other notes remain the same. Play through this C Dorian fingering and then listen to Clip 2, which runs through these notes over our C drone.
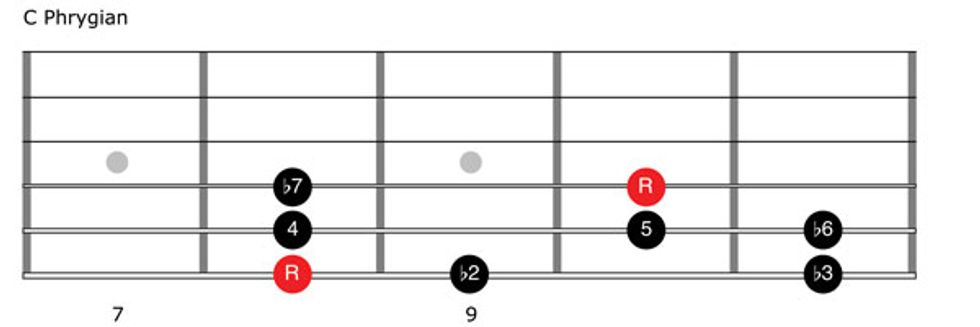
The Phrygian formula is 1–b2–b3–4–5–b6–b7–8, which means compared to the major scale from the identical root, we’re lowering four tones—b2, b3, b6, and b7. Listen to Clip 3 to hear C Phrygian, which is C–Db–Eb–F–G–Ab–Bb–C, as shown in Fig. 10.
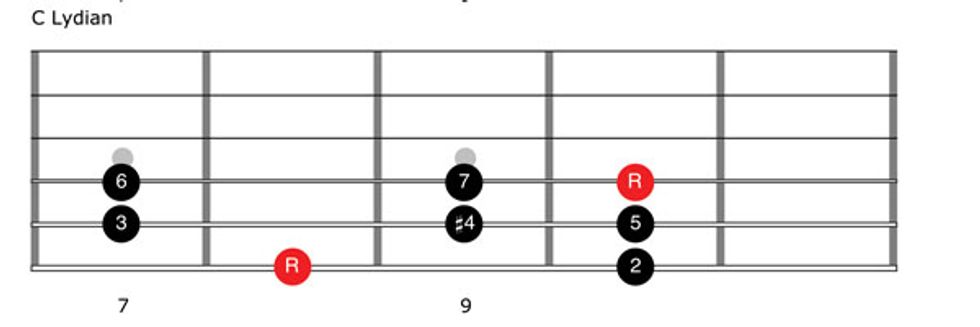
Things change with the Lydian mode. Rather than lowering any tones of the parallel major scale, in this case we raise the 4 by a half-step. This yields 1–2–3–#4–5–6–7–8. C Lydian is spelled C–D–E–F#–G–A–B–C, and you can see it in Fig. 11 and hear it in Clip 4.
The formula for the Mixolydian mode is 1–2–3–4–5–6–b7–8. Compared to its parallel major scale, only one note is altered—b7. This means C Mixolydian is spelled C–D–E–F–G–A–Bb–C. Check out Fig. 12 and Clip 5.
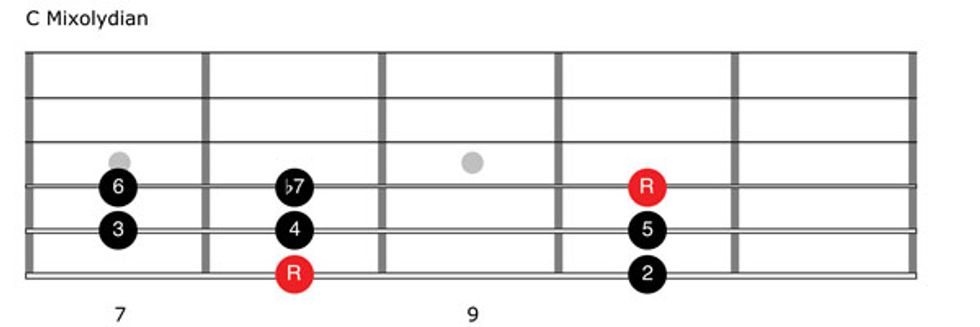
The Aeolian mode’s formula is 1–2–b3–4–5–b6–b7–8. Here we have three lowered tones (b3, b6, and b7) compared to the parallel major scale. Thus, C Aeolian is spelled C–D–Eb–F–G–Ab–Bb–C (Fig. 13 and Clip 6).
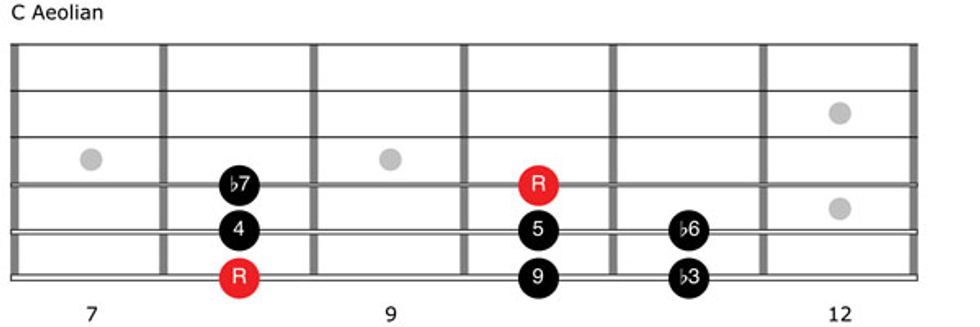
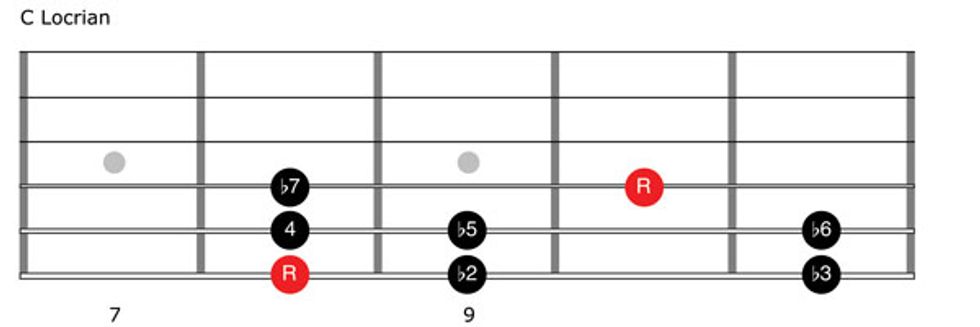
And our last mode is Locrian, which has a formula of 1–b2–b3–4–b5–b6–b7–8. That’s five lowered tones (b2, b3, b5, b6, and b7) compared to the parallel major scale. C Locrian is C–Db–Eb–F–Gb–Ab–Bb–C (Fig. 14 and Clip 7).
Relative or parallel: Which approach is better?
Because both ways of looking at the major-scale modes yield the same results, it comes down to which approach feels more natural to you. One is not better than the other, though it’s likely one will work faster for you, depending on the musical context and how you’re wired.
For example, let’s say you want to play D Dorian. Using the parallel approach, you’d simply take a D major scale (D–E–F#–G–A–B–C#–D) and modify it by applying the Dorian formula (b3, b7). This yields D–E–F–G–A–B–C–D, or D Dorian.
To calculate D Dorian using the relative approach, first think “Dorian means starting on the second degree of its relative major scale. D is the second degree of what scale? Oh yeah, that’s a C major scale or C–D–E–F–G–A–B–C. Now I simply need to shift over to the D root and run the same notes, which gives me D–E–F–G–A–B–C–D.”
Same outcome, different systems. It’s probably fair to say that most experienced improvisers—jazz musicians, for instance—think in terms of modal formulas, which is the parallel approach. (Of course, the most advanced players can run every mode in every key without having to even think about it.) But there are times when the relative approach makes sense. If you want to play G Locrian, it might be faster to think of G as the seventh degree of the Ab major scale and then run through Ab major using G as the root.
It’s wise to learn both approaches, so the next time someone says “play F Lydian in the solo section” and then counts off the tune, you have two options for coming up with the right notes: F–G–A–B–C–D–E–F.
Got a question for the Sensei? Email us at sensei@premierguitar.com.